推荐算法全系列
前言
本文是推荐算法系列第二篇:协同过滤算法。看懂本文需要懂矩阵、向量。
协同过滤算法理论基础
协同过滤算法是目前应用最成熟、最广泛的推荐算法之一,与基于内容的推荐算法不同,协同过滤算法不仅仅依赖用户自己的喜好,更依赖其他用户的喜好。协同过滤算法分为基于用户的协同过滤算法和基于物品的协同过滤算法。基于用户的协同过滤算法是指,用户在使用推荐系统的过程中,其所产生的历史行为,均会被看作是评分信息,协同过滤算法利用这些评分信息,找出与目标用户有相似兴趣爱好的若干个用户,这些用户被称为近邻用户,由于有相似爱好的人群,其所喜爱的物品往往是一样的,所以通过近邻用户的爱好来预测目标用户对某些物品的喜好程度,并将预测评分较高的物品推荐给目标用户。基于物品的协同过滤算法与基于用户的协同过滤算法同理,只是寻找相似用户变成了寻找相似物品。
以基于用户的协同过滤算法为例,对上述过程做一个直观化的理解,假设下表为用户User1、User2、User3对物品Item1、Item2、Item3,Item4的评分信息表,数字越大代表评分越高,为空则代表尚未进行过评分:
| Item1 | Item2 | Item3 | Item4 | |
|---|---|---|---|---|
| User1 | 5 | 4 | ||
| User2 | 5 | 3 | 5 | |
| User3 | 0 | 1 | 3 | 1 |
要为User1推荐一个物品,那么首先要找出与User1有相似爱好的用户,可以看到User2和User1对Item1和Item2的评分都比较高,而,User3的评分则比较低,于是选取User2为近邻用户,而User2对Item3的评分比较高,为5,那么预测User1度Item3的评分也为5,将5写入到User1对Item3的评分中,Item3即为推荐结果。
与基于内容的推荐算法相比,协同过滤算法不依赖于内容提取,从而避免了因内容提取不准确而导致的推荐不精准问题,同时,通过对评分的预测,也有助于提高推荐的惊喜度,可能会挖掘出用户潜在的兴趣。
本课题将改进和实现基于用户的协同过滤算法,来实现资讯的有一种推送方式。
基于用户的协同过滤算法的实现过程可以分成以下几个步骤:
(1)构建数据模型。在本课题中,协同过滤算法的输入应当是用户对资讯的评分数据,单个用户的评分数据可以看作是评分向量,而多个用户的评分数据则可以看成是评分矩阵,例如上面的评分表可以看作是如下的一个评分矩阵:

(2)计算相似度。这一步要在评分矩阵的基础上,计算其他用户与目标用户的相似度。相似度的计算方法有很多,本课题涉及到余弦相似度、皮尔逊相关系数、杰卡德系数和欧几里得距离。
余弦相似度是通过比较两个向量间的夹角的余弦值来度量相似度的,两个向量先做点乘,再用点乘积除以两向量模的积,即可得到两向量夹角的余弦值,余弦值越大,说明夹角越小,也就越相似。余弦相似度的计算公式如下:
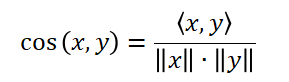
余弦相似度有其优点,那就是简单,一般可用于矩阵较为稀疏的情况中。但是余弦相似度也有其不可忽视的缺点,那就是无法解决向量平移问题,一旦向量发生了平移,其相似度肯定是改变了,但是计算结果却没有改变。
皮尔逊相关系数可以解决余弦相似度的不足,对于余弦相似度的平移不变性,可以让每个向量减去这个向量均值组成的向量来解决。皮尔逊相关系数是在两变量的协方差的基础上,再除以两个标准差之积得到的,也就是说,他是在协方差的基础上进行了标准化。皮尔逊相关系数的计算公式如下:
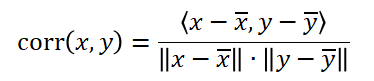
在推荐系统中,皮尔逊系数用的比较多,其值在0到1之间,值越高,代表相似度越高,一般高于0.6才会被考虑推荐,不过根据实际情况会有调整。
杰卡德系数则比较容易理解,他是计算两个集合交集占两个集合并集的比例,其计算公式如下:
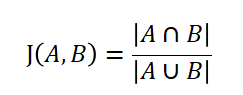
杰卡德系数的值越大,说明两个集合的相似度越高。
欧几里得距离,又称欧氏距离,他是一种距离度量,衡量的是多维空间中各个点之间的绝对距离,其计算公式如下:
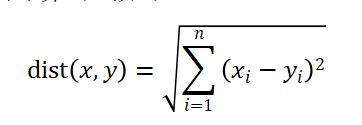
与上述几种相似度计算方法不同,欧几里得距离的值越小,相似度越高。
(3)选择最近邻。在相似度计算完成后,会得到相似度矩阵,在特征空间里面,利用最近邻的方法找到最近的若干个邻居,下图给出一个特征空间示例图:
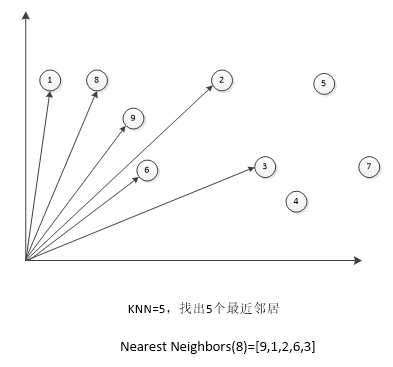
在这个特征空间中,找出8的五个最近邻居,就是看其他邻居与8的夹角,夹角越小,距离越近,所以结果是Nearest Neighbors(8)=[9,1,2,6,3]。
选取出来的最近邻将成为后续评分预测的关键,最近邻的数量也是一个值得探讨的问题,他并不是一成不变的,一般来说,数据量增大,最近邻的数量也应该随之增大,实际数量的多少应该根据实验的表现来不断调整。
(4)做出评分预测。当最近邻选择完成后,就需要将对应物品的评分相加,进行物品评分排行,将评分排行靠前的若干个物品推荐给用户,其评分预测可以通过平均值的方式获得。
基于mahout的协同过滤算法实现
目前有许多的开源算法库可以实现协同过滤算法,本课题基于mahout算法库的Taste组件,加以改进实现协同过滤算法库。
mahout提供了许多机器学习领域中的经典算法,并且支持算法的扩展。mahout中的Taste组件封装了多种推荐算法的实现,并且具备较好的扩展性,既提供了协同过滤算法的接口,又提供了一些扩展接口,使得用户可以定义自己的推荐算法。Taste的工作流程如下图所示:
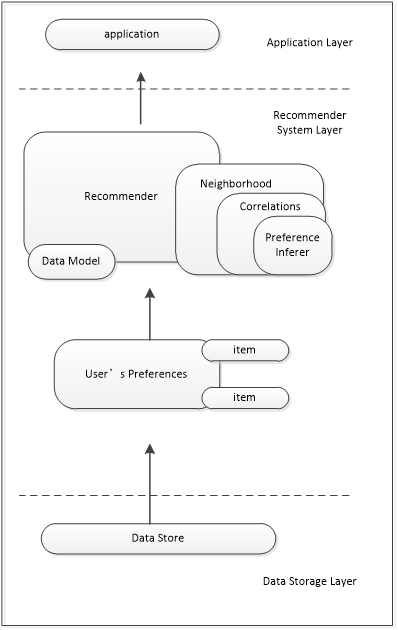
使用teste组件做推荐,主要分为四个步骤:
第一,构建DataModel,DataModel是用户喜好信息数据模型,Taste提供了JDBCDataModel和FileDataModel,分别支持从数据库和文件中读取用户喜好信息。
第二,定义相似度:分为UserSimilarity 和 ItemSimilarity,分别是用户间的相似度和物品间的相似度。
第三,构建最近邻Neighborhood,一般需要通过上一步定义的相似度来获得。
第四,进行推荐,使用Recommender接口,主要使用他的实现类GenericUserBasedRecommender 或者 GenericItemBasedRecommender,分别实现基于用户相似度的推荐引擎或者基于内容的推荐引擎。
改进的协同过滤算法实现
协同过滤算法在实际应用中经常面临一个问题,就是稀疏矩阵的问题。协同过滤算法的输入数据是用户对物品的评分信息,然后再将评分信息转化为评分矩阵,从而进行后续的计算工作。但是在实际运用中,由于系统运营时间较短或用户数量不足等原因,经常会遇到评分信息不足或较为分散的问题,这会导致其生成的评分矩阵成为稀疏矩阵。如果一个评分矩阵过于稀疏,那么就很难找到与目标用户特别相似的用户,这可能会导致近邻用户的数量不足或相似度不高,最终影响到推荐的结果。
本课题提出一种预测填充算法,来缓解稀疏矩阵问题。
要想缓解矩阵的稀疏性,首先想到的是对矩阵进行一定的填充工作,来增加矩阵中非零元素的数量。但是由于没有额外的评分信息可供使用,所以只能通过评分预测的方法来填充矩阵。可以使用基于物品的协同过滤算法来实现评分的预测填充,在进行协同过滤算法推荐时,要设定一个稀疏度阈值,当评分矩阵的稀疏度低于这个阈值时,认为该评分矩阵为稀疏矩阵,应该进行评分预测填充,降低稀疏度之后再进行推荐。改进的协同过滤算法设计过程如下:
输入(INPUT):评分矩阵,目标用户u,邻居数量S,稀疏度阈值Y,推荐数量N。
输出(OUTPUT):推荐结果集合RS。
运算流程(PROCESS):(1)计算评分矩阵的稀疏度,如果大于稀疏度阈值Y,跳转至步骤(5),否则不进行跳转。(2)对于仍有剩余评分位置的文章a,计算a与其他文章的相似度,选择相似度最高的前S个文章作为a的邻居文章。(3)对于a中空缺的评分,利用a的邻居对应评分的平均值作为预测值,填入到评分矩阵中。(4)重复步骤(2)-(4),直到所有符合条件的文章都已进行过评分预测。(5)根据评分矩阵,计算其他用户与目标用户a的相似度,取相似度较高的前S个用户作为u的邻居用户。(6)根据u的邻居用户的评分信息,对所有u未评价的文章进行评分预测。(7)将预测结果按照预测评分值进行排序,取前N项作为推荐结果。
算法的流程图如下:
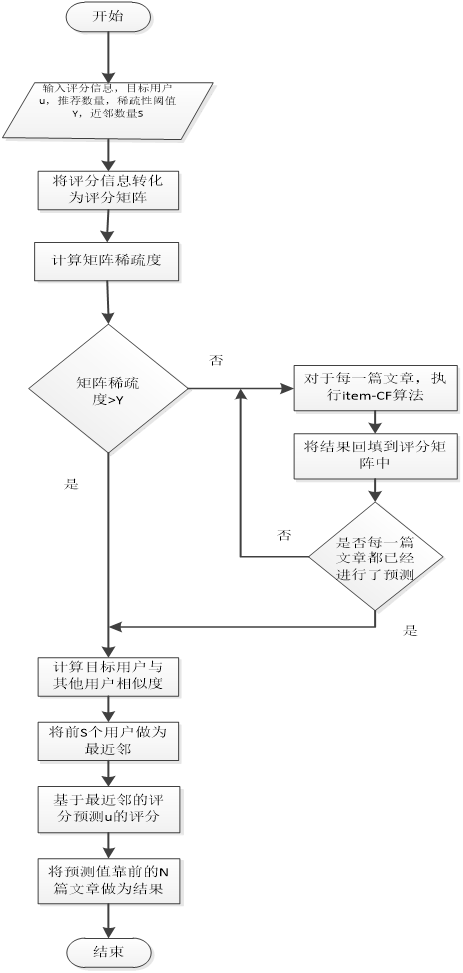
至此本课题的协同过滤算法设计完成,在实现该算法时,只需要在mahout Taste组件的基础上,添加降低矩阵稀疏度操作的代码即可。
算法评价
这里介绍两种算法评价方式:均方根误差和平均绝对误差
均方根误差和平均绝对误差
均方根误差,是用来衡量预测值与真值之间误差的一个指标,常用来作为机器学习训练模型的评价指标。它的值是通过计算预测值与实际值之间差的平方,取平均数之后再开根得到,计算公式如下:
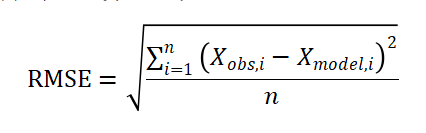
上式中,为真值,为预测值。均方根误差的计算过程和标准差的计算过程类似,但是二者作用的对象不同,均方根误差衡量的是预测值与实际值的误差,而标准差是用来衡量一组固定数值的离散程度。
平均绝对误差是预测值与实际值之间绝对误差的平均值,它可以避免误差之间相互抵消的问题,其所反应的误差值往往更加真实,计算公式如下:
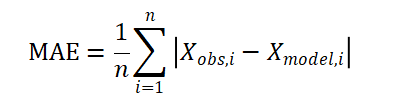
均方根误差和平均绝对误差的值越接近0,说明误差越小。均方根误差相当于L2范数,平均绝对误差相当于L1范数,范数越高,计算结果就越会受到较大值的影响,所以当样本中一个预测值与实际值偏差很大的时候,均方根误差的值会比平均绝对误差高出很多。由此可见,均方根误差更能突出反应偏差较大的情况,而平均绝对误差则能够反映真实的偏差,二者结合可以取长补短。








高谈阔论