推荐算法全系列
正文
在推荐系统中,尤其是含有内容推荐的系统,对用户兴趣的刻画至关重要,用户兴趣模型的好坏直接决定着推荐的精准度。用户的兴趣可以分为长期兴趣和短期兴趣。所谓长期兴趣,就是用户所具有的一种相对较为稳定和持久的喜好,比如对于球迷来讲,他们对球星、球类赛事等能保持相当长一段时间的喜好。而短期兴趣则不同,短期兴趣是不稳定的,它往往出现的很快,消散的也很快,例如,一个普通用户,它并非球迷,但由于受到世界杯热度的影响,也会去观看相关赛事,但随着时间增加,世界杯结束,该用户也不再去关注球类的信息,这便是一种短期兴趣的表现。由此可见,用户的兴趣并非一成不变,它总会随时间而变化,其所呈现的基本规律是:长期兴趣相对稳定,短期兴趣则会一直更替。本节将探讨用户兴趣与时间之间的衰减关系。
先做出这样一个假设,如果不对用户的兴趣模型做任何的干预,那么随着时间的推移,用户不断汲取与长期兴趣有关的内容,长期兴趣的权重将变得越来越大,这势必会对其他兴趣产生覆盖效果,而对于短期兴趣,由于一些短期兴趣没有得到衰减,它仍然拥有较大的权重,那么新出现的短期兴趣便会被掩盖,且给用户推荐的内容中存在一些用户已经不感兴趣的内容。到此我们得出结论,要想实现长期兴趣的稳定和短期兴趣的更替,需要引进用户兴趣衰减模型,让所有的兴趣随着时间推移而衰减,如此一来,长期兴趣会不断有权重加进来,总权重可以保持稳定,而过时的短期兴趣由于没有得到补充,将会一直衰减,其权重会越来越小,当衰减到一定的阈值时,我们便认为用户不再具有这一兴趣。新出现的短期兴趣由于没有进行长时间的衰减,所以可以保持一个较高的权重。
至此问题转化为如何建立一个合适的时间衰减函数。这里,本课题将借鉴物理学中的牛顿冷却定律来建立用户兴趣衰减模型,这也是利用物理学的方法来指导软件的研究工作。
牛顿冷却定律一般都是用来建立与时间有关的衰减模型上,在新闻资讯领域,随着时间的增加,用户对某类资讯的兴趣衰减就可以用牛顿冷却定律,或者牛顿冷却定律也可以用在某一篇新闻的热度衰减上。
牛顿冷却定律模型描述的是,一个比较热的物体(高于环境温度),随着时间增加,是会逐渐冷却,直至与环境温度相同,在这个变化过程中,是有规律可循的,伟大的物理学家牛顿在1701年用实验证明,物体温度的降低速率和当前环境温度的差成反比例关系,用数学的方法表示出来就是:
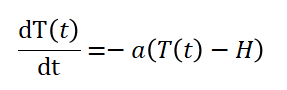
其中,T(t)表示物体当前温度,H为环境温度,a为比例系数。上述公式可以看成是一个微分方程。下面对这个微分方程进行求解,先对上式做一个变换:
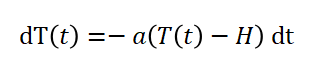
对上式再进行变换,并对两边求积分:
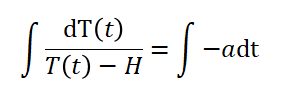
由于:
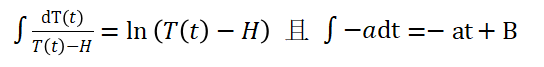
所以:
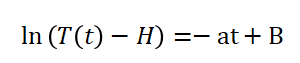
其中B是微分方程的求解因子,对上式再进行转化可得:
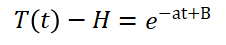

上式还存在一个变量C待求解,我们可以根据初始条件求解,假设t0为初始时刻,那么:
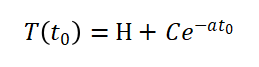
求解上式可得:
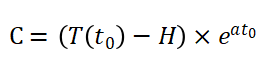
把C的表达式带入到求解公式中就可以得到:
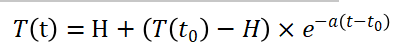
由于我们希望兴趣最终衰减的方向为0,所以令H=0时,就可以得到最终公式:
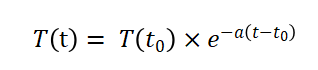
其中a时自己设定的衰减系数,当经过t时间后,物体的温度是初始温度和衰减速率的乘积。
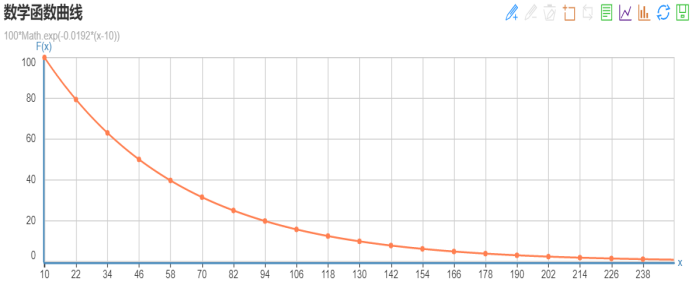
这个公式应用在兴趣衰减中时,只需要设定合适的衰减因子a即可,如果希望兴趣衰减的快一些,那么衰减因子a就取较大的值,否则就取较小的值。以初始兴趣权重为100,初始时间为10,衰减因子为0.0192为例,其衰减曲线如下图所示:








高谈阔论